【はじめに】
クロスワード、ジグソーパズル、ルービックキューブ、そして数独。楽しいパズルは年齢、性別、言語、文化、宗教の違いなどものともせず、軽々と国境を越えどこまでも浸透していく。イギリスのパズル作家ヘンリー・アーネスト・デュートニーは「パズルを解くことは人間の根本的な性（さが）である。」と言っている。おそらくパズルを解く能力は長い進化の中で有利に働き、ホモ・サピエンスの遺伝子にしっかりと生き残ってきたと思われる。

2005年、数独は突然、世界的な大ブームになる。私は期せずしてその渦中に立たされ、燎原の火のごとく数独が広がっていく様を唖然として眺めていた一人である。もしこれが病原菌だったら、世界の人口は半減していただろう。職場でも、居間でも、酒場でも、人々は集まると数独の話をし、世界中の新聞に数独が毎日掲載された。この年の9月、日本では衆議院議員総選挙が行われ、時の首相小泉純一郎は郵政民営化を前面に押し出し圧勝した。確か、ロンドンのThe Timesであったか、「小泉は数独のように勝利した。」と見出しに書かれたのを覚えている。

それから十数年が過ぎ、今も世界のほとんどの国で、数独の魅力にとりつかれ、日々解きまくっている人たちがいる。合計で間違いなく数千万人はいるだろう。あるいは電車を乗り過ごし、あるいは寝不足に悩まされ、それでもいつの間にかまたもう一問、彼らは没入していく。優れた発明の多くが、一人の天才のひらめきよりも、大勢の人たちの小さなアイデアとカイゼンの積み重ねで生まれるように、数独もいくつもの情熱と偶然でここまでの市民権を得てきた。それを「数独物語」と題してこれから書き始めていきたいと思う。

 

【第1章】数独のルーツ
～中国の占いから生まれた数独の原型～

古い言い伝えによれば、紀元前2000年、後に中国最古の王朝といわれる夏王朝の始祖となった禹（う）帝が治水工事の際、川から上がってきた亀の甲羅に奇妙な文様があるのに気付いた。それは下図のような模様であった。そしてこの白丸、黒丸のひとつながりを個数として置き換え、漢数字で表すと右の表が得られた。

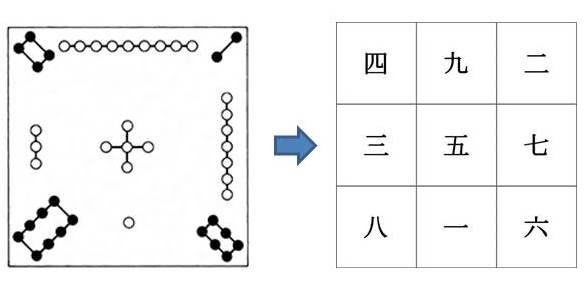
この表のどのタテ列、ヨコ列も足すと合計は15になる。更に、斜めにも足してみると15になる。（4+5+6=15；2+5+8=15）　禹帝はこの数字の配置に何か神秘性を感じ、これは世界の理（ことわり）、宇宙の秩序を表しているのではないかと考え、「洛書（らくしょ）」と名付け、占いの道具として珍重した。3×3のマスの中に1から9の数字がひとつずつ入っている。今から4000年も前に数独のルーツが生まれていたのである。

洛書は、やがて占星術と結びつき、生まれの年月日と組み合わせ、九星術という占いに発展していく。日本でも九星気学と呼ばれ、一白水星、四緑木星など現代でも運勢、家相を占うものとして使われている。

日本数独協会に愛知県にお住いの方から一枚の写真とともに、お問い合わせをいただいたことがある。「これは祖父が残したもので、厚さ35ｍｍの木の板に数字が彫られています。一体何でしょうか。」写真を見ると、9×9のマスの中に1から9の数字が入っており、更に、3×3のブロックになっている。世界最古の数独の原型ではないかと、盛り上がり、ホームページに掲載したところ、長野県在住の方より、これは九星気学で使う、「後天定位盤」であるとのご指摘を受けた。まさに、数独のルーツここにありと思わせる逸品である。

さて、禹帝の洛書はヨーロッパに伝わり、「Magic Square」と呼ばれるようになる。一方、日本では江戸期になって、和算の大家、関孝和が数学の対象として研究し、「方陣」と名付けた。明治になって、西洋から入ってきたMagic Squareと関孝和の方陣が一緒になり、「魔方陣」と呼ばれるようになる。現在では一般的に使われているので、ここでも以後、魔方陣という名で話を進めていく。

遠く禹帝が宇宙の調和を感じたように、魔方陣はヒンドゥー教、イスラム教、ユダヤ教、そしてキリスト教にも影響を与えた。御守りや魔除けとして、図案化され、出征する戦士の上着に刺繍されたという記録も残っている。ルネサンス期に入り、人々の発想がしなやかになってくると、魔方陣を4×4にしたらどうなるかと、考えた人がいた。ドイツの画家であり、数学者であったアルブレヒト・デューラー（1471～1528）である。彼の作品の中で「メランコリアⅠ」という銅版画がある。大変不思議な絵で、風景画でも、人物画でもない。画面中央には背中に羽の生えた女性が頬杖をついて何か考えている。周りには妙な動物、砂時計、立体などが散らばっており、女性の後ろの建物の壁には数表が彫られている。それが下図である。

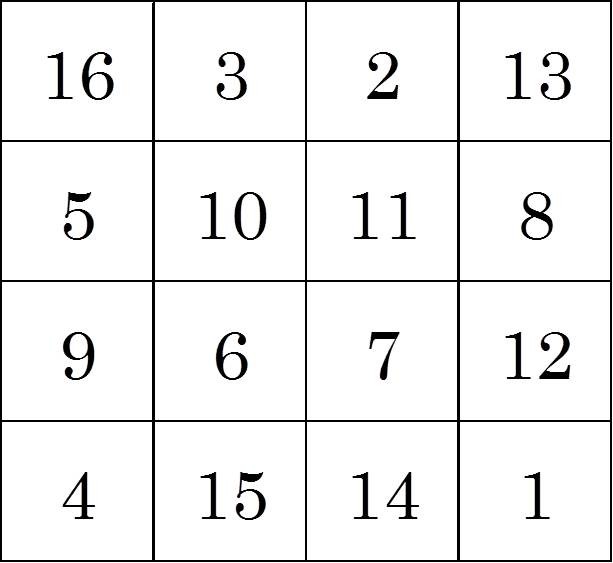
4×4の正方形の中に1～16の数字がひとつずつ配置されており、どのタテ列、ヨコ列、そして斜めも数字の和は34になる。これだけではない。デューラーの魔方陣には驚くべき秘密が隠されている。下図のように、盤面の中から4点を選び、線で結んで四辺形を作る。この四辺形の頂点の4つの数字の和がすべて34になるのだ。更に横一列目の数字の平方数の和と横二列目の平方数の和は、横三列目と横四列目の数字の平方数の和に等しく、それは対角線の二列の数字の平方数の和にも等しい。一番下の列の二つの数字、15と14は、この銅版画の制作した年、1514年というのだから、念が入っている。人間業とは思えない、まさしく魔の方陣である。

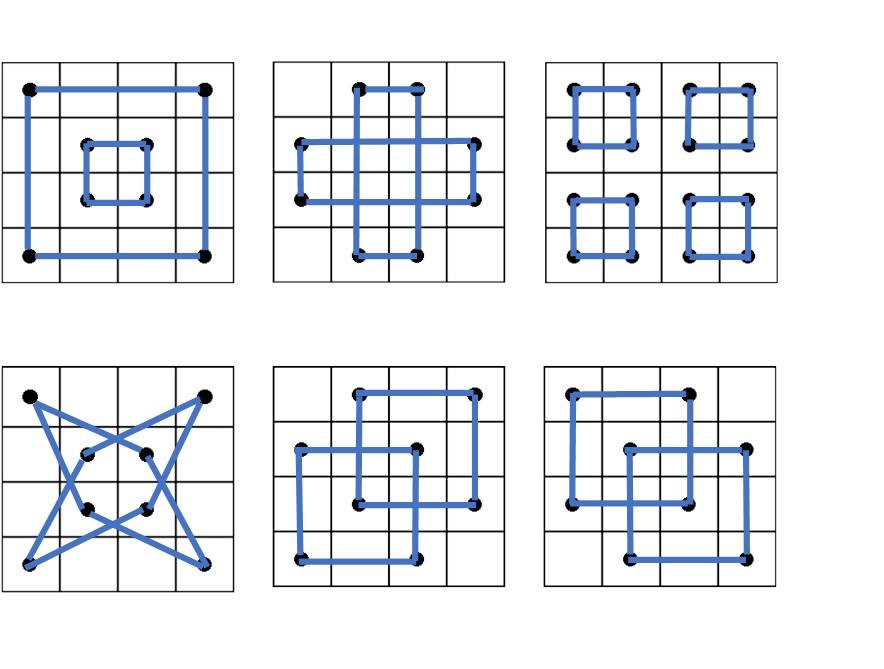
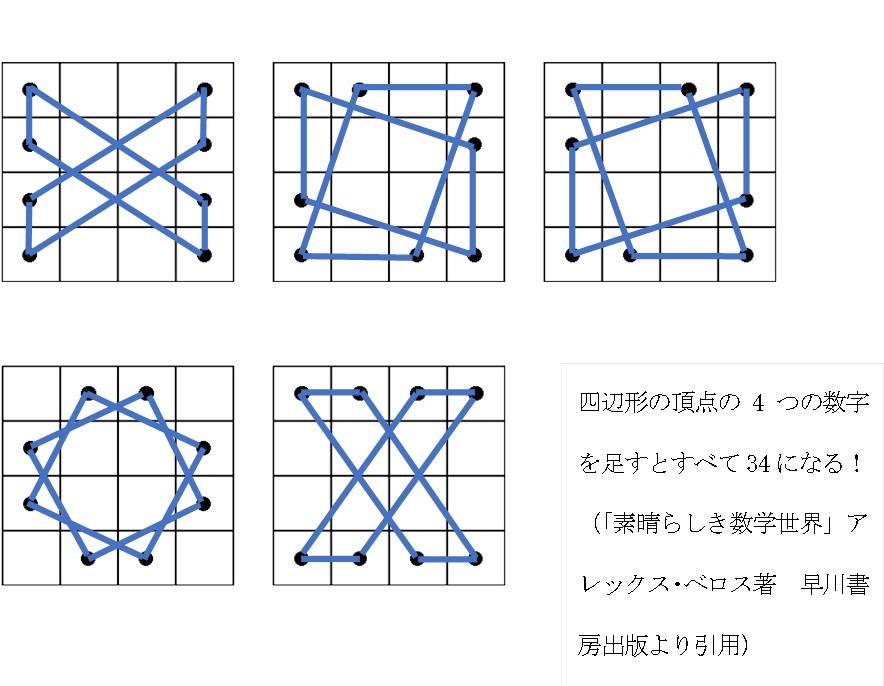
近世数学の夜明けとともに、魔方陣も数学の研究対象となった。そもそも数学というものは、数字を使って羊の数を数えたり、財産の分与を計算したり、土地を測量したりという実用的な目的のための道具であったはずなのだが、やがて、円周率を果てしなく追いかけるなど、数学で解決するべき問題が数学の中から生まれることになってくる。同じように、魔方陣も占いという実用的な要素が失われ、数学者の格好の研究素材として料理されることになる。

先ずは、魔方陣を自ら作ってみるところから始まった。3×3では組み合わせはどうやっても1通りである。4×4になると、880通りもあることが分かった。前述のデューラーの魔方陣もこの中の一つである。5×5の正方形のマスに1～25の数字が一つずつ入り、各タテ列、ヨコ列、そして斜めの数字の和が65になる魔方陣を作ろうとして、あまりにもその数が多いので行き詰まった。これは、1970年代になってコンピュータで計算してようやく判明するのであるが、当然、当時の人たちには推測もできなかったであろう。答えは2億7500万通りを越えるのである。（ちなみに6×6では1の後ろにゼロが19個並ぶ数だそうである）。また、素数だけを使った素数魔方陣、平方数だけを使った平方魔方陣というのも生まれた。そのような中で、スイスの著名な数学者レオンハルト・オイラー（1707～1783）は晩年、視力を失ってから魔方陣に興味を持ち、「ｎ行、ｎ列の表の中に、1からｎの異なる数字を、各行、各列に重複しないように並べる」というルールの方陣を考えた。図に描くと以下のようになる。

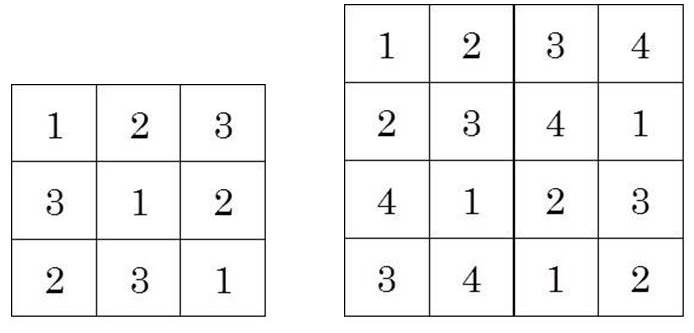
オイラーはこれを「ラテン方陣」と名付けた。数独ファンならば、この「各行、各列に重複しないように」というフレーズに、思わず反応したことだろう。魔方陣から足し算が消え、数独の原型とも言える考え方が生まれたのである。

それから100年以上が経ち、19世紀も終わる頃の1895年7月6日、フランスの新聞－ラ・フランス－にこんなパズルが掲載された。

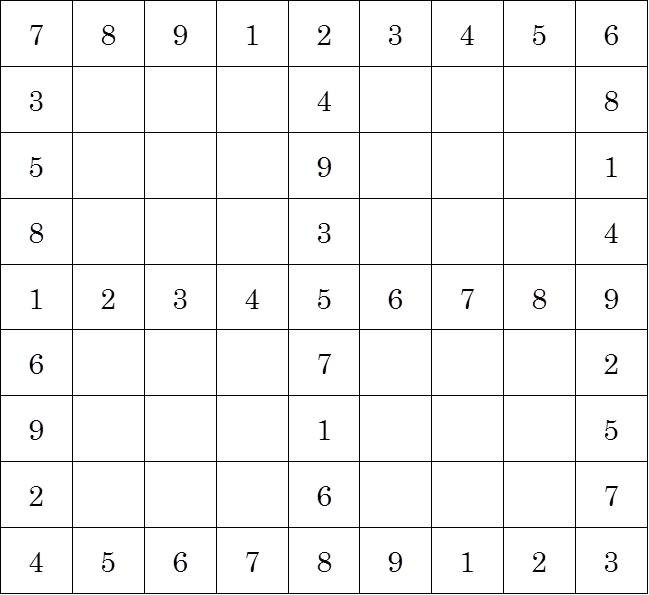
９×９の盤面に最初にいくつかの数字が並んでおり、各タテ列、ヨコ列に1から9の数字を重複しないように入れていくというパズルで、正にこれは9×9のラテン方陣である。しかしながら、実際にこのパズルを解いてみると、論理的に追い詰めていくというより、仮の数字を置いては、トライ・アンド・エラーを繰り返すというかなり苛酷な作業である。ラテン方陣を数学の対象から娯楽の範疇に引っ張り込んだ歴史的作品ではあるが、パズルとしては失敗作で、人々の支持を得ることなく消えた。

アメリカにデル・マガジンズ（Dell　Magazines）という出版社があった。設立は1921年というから、ちょうど第一次大戦と第二次大戦の間である。発売当初はミステリー集やユーモア集などを刊行していたが、折からのクロスワードパズルのブームに乗り、パズル誌を発行するようになる。その後、同じパズル誌を出版するペニープレス社に合併吸収されるが、雑誌のタイトルに「デル」の名は今も残っている。

さて、このデル・マガジン社発行の雑誌「ペンシルパズルス・アンド・ワードゲームズ」1979年5月号に「ナンバープレイス」というパズルが掲載された。今から40年近くも前のことである。

ルールを読むと、各タテ列、各ヨコ列そして小さな9つのボックスの中に、1から9の数字を重複しないように入れなさい、と書いてある。全く数独と同じ盤面、同じルールである。即ち、数独がこの世に誕生した瞬間である。この問題には更にヒントとして、盤面の中に丸印があり、ここから始めると解きやすいですよと、入る数字まで示されている。数独ファンのみなさんには、このヒントに従い丸印から先に数字を入れ、是非最後まで解ききって欲しい。これがあなたを虜にして離さない数独の、世界最初の問題である。

ところが、この「ナンバープレイス」というパズルは、当時のアメリカではほとんど人々の関心を引かず、わずか数年で姿を消すことになる。そのため、このパズルを誰が考案したのか、それさえも話題にならなかった。

後に、数独が世界的なブームになったとき、ニューヨークタイムズのパズル編集長ウィル・ショーツがこの調査に乗り出した。「『ペンシルパズルス・アンド・ワードゲームズ』という雑誌は巻頭に、パズル作家の名前の一覧表があるだけで、誰がどのパズルを制作したのか特定することができなかった。そこで私は1979年から1980年代全部の雑誌をくまなく調べ、一人の名前にたどり着いた。」とショーツは語っている。その名前がハワード・ガーンズ（Howard　Garns）である。「ナンバープレイスが掲載されている号には、ハワードの名前があり、逆に掲載されてないときにはハワードの名前がなかった。」

彼こそが、9×9のラテン方陣を3×3のブロックで9つに分割し、更にそのブロックの中も1から9の数字を重複させないように入れるというアイデアを考え出した人物である。ショーツは「ハワードは８０年も前のフランスの新聞は見ていないだろう。ただラテン方陣については知識があったと思われる。」と言っている。残念ながら彼は癌を患い1989年にこの世を去っており、何をもととして、このアイデアに至ったかは不明であるが、少なくとも、ラテン方陣に制約を加えることで、入れられる数字が限定され、それがロジックパズルとなること、その論理性の美しさに気がついていた人であろう。

ハワード・ガーンズは1905年アメリカ・インディアナ州コナーズビルに生まれる。父親は建築家で、その影響でイリノイ大学では建築学の修士を取得、卒業後も父の経営する会社で働いていた。第二次世界大戦が始まると、空軍省で技術者として勤め、大佐にまで昇格した。戦後は建築会社に就職し、定年まで勤め上げる。数学にも、パズルにも、出版にも全く縁のない人生を過ごしてきたのである。そして退職後、ようやく趣味であったパズルに没頭する時間が持て、74歳のときに、デル社のマガジンに生涯の傑作「ナンバープレイス」を投稿したのである。

しかし、既に述べたように、これほどのパズルがほとんど誰にも注目されず、数年間でわずか1ダースほどの作品が発表された後、掲載が中止となった。（あるいは、ハワード自身が病に冒され、作品が作れない状態だったのかも知れない）。そのままであれば、ナンバープレイスは数多あるペンシルパズルの一つとして、歴史の中に埋もれてしまう運命だった。

ところが、ここで奇跡が起こった。太平洋を隔てた、極東の島国でこのパズルをたまたま解いた男がいたのだ。

1980年、日本で最初のパズル誌が生まれた。現在では大概の書店にパズルコーナーがあり、様々なパズル雑誌や書籍が並んでいるが、当時はパズルといえば、せいぜいクロスワードパズルが、新聞や雑誌の片隅に懸賞用に掲載されている程度であった。

印刷会社の社員であった鍜治真起がまるまる一冊、パズルだけの雑誌を作ろうと思い立ったのは、彼自身がパズルに興味があったわけではなく、第2章に登場したデル社のパズルマガジンを見て「アメリカで売れるなら、日本でも売れるかも。」という単純な理由であった。出来上がったのが「パズル通信ニコリ」である。1980年5月に創刊準備号、8月に創刊号が発売されている。

私と鍜治は高校時代の同期生で、卒業から10年も経った1980年の正月にたまたま鍜治宅に当時の悪友達が集まった。その時、鍜治がおもむろに取り出したのがこの創刊準備号なるものであった。色ムラのあるペラペラの表紙に手書きのクロスワードと迷路。どうみても素人の同人誌である。「俺はこの雑誌で商売をしようと思っている。」と鍜治が言ったとき、集まっていた仲間全員が声を揃え「こんなものは絶対に売れない。」とブーイングをしたのを覚えている。ところが友人達の予想は見事に外れ、「パズル通信ニコリ」は売れてしまったのである。部数は号を追うごとに伸び続け、不定期だった刊行は年4冊の季刊となり、3年後の1983年、鍜治は株式会社「ニコリ」を設立し、本当にパズル誌を商売にしてしまったのである。

ニコリのゲリラ的な成功は、それまでパズル誌に躊躇していた出版社を大いに刺激した。千代田区に本社ビルを持つ世界文化社が、大手出版社らしく、アメリカ・デル社と提携を結び、パズルの掲載権を得た上で、1983年12月に雑誌「パズラー」を発売する。この時、アドヴァイサーとして動いたのが当時フリーライターであった西尾徹也である。西尾は27～28歳頃からパズルに興味を持ち始め、丸善の洋書コーナーでデル・マガジンを買い求めては、解いたり、作ったりを繰り返していた。

つまり、鍜治も西尾もデル社のパズルマガジンを参考にしながら、日本にパズル文化と呼べるものを作ろうとしていた。そして迎えた1984年、彼等二人は、まるで示し合わせたかのように、一つのパズルをデル・マガジンの中から発見する。それが、ハワード・ガーンズ作「ナンバープレイス」であった。面白いことに二人とも英語は苦手なのだが、このシンプルなルールはすぐに理解でき、あっという間に解いてしまった。解くだけではなく、早速自らで作って見た。

最初に発表したのは鍜治である。1984年4月「月刊ニコリスト」に自作のナンバープレイスを掲載した。その際、このパズルを「数字は独身に限る」と命名した。各列、各ブロックに1から9の数字が一回しか入らない。一回はシングル、シングルは独身という発想である。このネーミングの妙が、後々世界を駆け巡るネタになるとは、当然のことながらこの時彼はまだ知らない。

一方、西尾は創始者ハワードに敬意を表しタイトルは「ナンバープレイス」のまま、同年10月雑誌「パズラー」に自作を発表する。以後、「数字は独身に限る」は「数独」となり、「ナンバープレイス」は「ナンプレ」と縮められ、多くのファンを獲得していくことになる。

鍜治真起はパズル誌専門の出版社の社長でありながら、パズルを解いたり、作ったりする才能には恵まれていなかった。本人がそのことを一番良く知っていたので、彼は読者を如何に巻き込むかということをいつも考えていた。読者から投稿作品を募り、その作品を掲載することで販売部数を伸ばし、投稿者の中で優秀な者たちを作家として囲い込み、更に優秀な作家を社員として迎え入れた。結果、ニコリ社は作家集団となり、ニコリ誌はパズル作家の登竜門としての地位を築いた。

数独の場合も鍜治が自作を発表した途端、読者から投稿が殺到し、一躍人気パズルとしてニコリ内では不動の位置を占めるようになる。（下の写真は鍜治が発表した日本最初の数独である。コメントに注目してみると、「誰か作って。」と彼はしっかり催促している。）

これに対し、西尾徹也は「お絵かきロジック」という大人気のパズルを考案するなど、ロジックパズルの天才であり、後に西尾自身の傑作を集めた「世界一美しく難しいナンプレ」を刊行するのだが、同時に雑誌「パズラー」誌上に「激作塾」という投稿先品を募るコーナーを主宰し、若手パズル作家の育成も目指した。

数独もナンプレも作り手が増えることにより、次々と新しいテクニックが開発され、そのテクニックを使わないと解けない問題が出題され、難易度は高まる一方であった。表出数字（問題に最初から現れている数字）も、これまでは作家が好き勝手にバラバラに配置させていたのだが、点対称、あるいは線対称に配置するというルールを作り手に課した。これによって、見た目の美しさということも評価のポイントとなった。数独の本質から言えば、表出数字が対称でなければならない理由はない。しかし、対称でない投稿作品を没にすることで、いつの間にか、対称であることが不文律となっていったのである。

こうして1988年、数独だけが掲載されている新書サイズ「ペンシルパズル本　数独」がニコリ社から発売され、世界文化社もすぐに追随し、新書サイズの「ナンプレ」を発行する。ともにシリーズ化され、書店の棚には、数独とナンプレがずらりと並ぶことになる。ハワード・ガーンズが蒔いた種が、5年の歳月を経て日本にたどり着き、そしてようやく花開いたのである。

ニュージーランド人で香港判事であったウェイン・グールドは、多忙で神経を使う仕事の合間にパズルを解くことが唯一の趣味であった。「答えがひとつしかないことが好きだった。」と彼は語っている。そんなウェインが判事を辞し、祖国ニュージーランドに帰る途上、日本に立ち寄った。1997年のことである。飛行機の中の退屈しのぎに何かよいパズルはないかと、書店のパズルコーナーを漁ると数独の本がずらりと並んでいた。もちろん日本語は読めなかったが、例題を見ただけでルールが理解できた。

ニュージーランドに戻ると、彼は数独の本を一冊しか買わなかったことを後悔した。一度書いた答えを全部消して、もう一度解いたそうだ。どうしてもこのパズルをもっと解きたいが、ニュージーランドでは売っていない。そこで彼は、鍜治や西尾と同じように自分で作ることを考えた。ただ、彼の場合、多少コンピュータの知識があったので、問題を自動生成するプログラムがあれば、いくらでも遊べると思った。つまりウェインは作ることではなく、解くことに興味があったのである。そこから2年の歳月をかけ、彼のプログラムはどうにか数独らしき問題を生成するようになった。そこで、これをインターネット上に公開し、他のプログラマーがどう評価するか試してみたくなった。ただその前に、この数独の本を作った日本のニコリという会社に敬意を表し、挨拶するべきと考えた。

1999年、私は財務兼海外担当というポジションで株式会社ニコリに入社した。昔「こんな本は売れない。」とケチをつけた出版社に自らが入ることになろうとは思ってもみなかった。入社早々飛び込んできたのが、ウェイン・グールドからのエアメイルである。礼儀正しい文章の自己紹介に続いて、インターネット上にsudoku.comというサイトを立ち上げたいので認めてほしいという内容であった。ニコリが所有していた商標登録は日本国内だけであったから、海外で「数独（sudoku）」の名前を使うことに対し、何か言える権限はなかった。もちろん、元香港判事はその辺もすべて調べた上で、仁義を切ってきたのである。「名前を使うことにNOとは言えないが、数独をプログラムで自動生成することには疑問がある。」というような返事をしたら、年を越した2000年2月、ウェインは日本に乗り込んできた。

会ったのは新橋のホテルだったと記憶している。「数独の問題は、一問、一問が個性的であるべきだ。プログラミングで生成した場合、一律的になってしまうのではないか。」これが当時のニコリ編集部の自動生成に対する考え方であった。それをウェインに告げると、彼は神妙な面持ちで考え込んでしまった。表出数字は点対称に配置すること、sudokuはスドクではなく、スウドクと発音することなどを私は彼に教えた。そして、ウェインは数独とナンプレの本を山ほど買い込んでニュージーランドへ帰って行った。

それから2年後、ウェインから数独の問題が添付されたメールが来た。「何が数独にとってエキサイティングかを私は研究した。是非、ニコリの人たちに解いていただき、その結果が聞きたい。今、私は日本にいます。」私たちは同じ新橋のホテルでビールを飲んだ。「あなたの問題は結構いいレベルに達しているとニコリでは評価している。」というとウェインはとても喜び、パソコンを取り出し、プログラムを走らせた。画面には数独の盤面が立ち上がり、F1ボタンを押すと、問題が瞬時に入れ替わる。「もう少し改善が必要です。」彼は目を輝かせてこう言った。

「数独の好きな風変わりなニュージーランド人」が私の中でほぼ思い出となっていた2004年暮れ、妙な話を耳にした。ロンドンで数独が流行っているというのだ。その前年の2003年に、私はイギリスを訪れ、老舗パズル出版社との契約に成功し、ニコリとの取引が始まっていた。しかし彼等は数独に興味がなかったので他のパズルを提供していた。早速提携先の会社に連絡してみると、「今、あなたにメールをしようと思っていた。タイムズ（The Times イギリスの全国紙）に数独が掲載され、それが人気になっている。」「どうして、タイムズに数独が？」「ウェイン・グールドという男が売り込んだようだ。」「ウェイン・グールド！」その時の衝撃は未だに忘れられない。

後にウェインと会って、彼から直接聞いた話だが、ウェインは初め、ニューヨークタイムズに売り込みに行ったそうだ。アポなしで突然訪ねたので、当然ながら玄関払いをくらい、編集部には会えなかった。（この時のニューヨークタイムズのパズル編集長は第2章に登場したウィル・ショーツである。もし、受付が面会を許していたら、どうなっていたのだろうか。）次に彼はロンドンに飛び、タイムズ社を訪ねた。彼はタイムズ紙のクロスロスワードが掲載されている部分を切り抜き、そこに自前の数独の盤面を同じ大きさにして貼り付けたものを用意していた。受付にそれを渡し、編集部に会わせて欲しいと頼んだが、ニューヨーク同様、追い返されてしまった。ところが、ホテルに戻ると、タイムズ社の編集部から電話がかかってきて、今すぐ会いたいというのだ。

2004年11月12日、タイムズ紙朝刊のパズル欄にウェイン・グールドのプログラムから吐き出された数独が一問掲載された。これが世界中に数独が広まる幕開けであった。一ヶ月もすると、sudokuという奇妙な名前も相まって、数独が人々の話題になりだした。明けて2005年、ロンドンはもうsudoku一色にそまり、「今朝のsudokuは解いたか？」が朝の挨拶になっていたという。タイムズ紙は一気に売上を伸ばしたが、すぐに他の新聞社も追いかけた。というのも、ウェインはsudoku.comというサイトを立ち上げており、その中で自前の数独プログラムを9.95ドルで販売していたのだ。新聞社はこれをダウンロードし、F1ボタンを押しては数独を生成していた。

イギリスの全国紙のすべてと、地方紙のほとんどすべてに毎日sudokuが掲載されだした2005年4月、私と鍜治は一体何が起きたのか知りたくて、ロンドンに飛んだ。提携先の社長が満面の笑みで「さあ、数独の契約をしよう！」と私たちを出迎えた。ウェインのsudoku.comでは、数独はジャパニーズパズルであり、ニコリ社のオリジナルパズルと書いてあったので、鍜治は数独の創始者として、また奇妙な名前の考案者として一躍、注目を浴びることになる。パブで飲んでいれば、サインや握手を求められ、「私の夫は数独に夢中で、私にかまってくれない。夫を帰せ。」とからまれ大騒ぎであった。

しかし、これは始まりのベルが鳴ったに過ぎない。本当のパニックはこれからだった。ロンドンからイギリス全土に、そしてアメリカ、カナダ、オーストラリア、インド、香港と旧大英帝国に数独の嵐が吹きまくると、これを知った日本の読売新聞社が記事にした。Yahooニュースでもトップを飾る記事となり、ニコリのサーバーにはアクセスが殺到し、パンクしてしまった。

もうそこからは何が何だか分からない。毎日のように、世界中のいろんな国から、問い合わせや、取材依頼が飛び込んでくる。数えてみたらその年の暮れまでに、53の国と地域からメールが来ていた。ニコリという会社そのものを買いたいという話やら、儲かったのだから寄付をしてくれというメールやら、アルジャジーラのTV局から取材の申し込みがあったのも驚かされた。鍜治はもはや売れっ子のタレントのように、テレビに、ラジオに、引っ張りだこで登場し、なぜかメンズ雑誌の表紙を飾る仕事まで舞い込んできた。

書店からの注文電話はひっきりなしにかかり、ゲームソフト、携帯アプリ、電子辞書、数独玩具、数独Tシャツついには数独チョコレートまで発売された。一過性のブームかと思ったが、なんとこの状態がほぼ3年続いた。数独のブームは社会現象とまで言われるようになり、ちょうどこの頃から始まる脳トレとのコラボレーションは2006年のヒット商品番付で東の横綱に選ばれた。

スペインの大学医学部の授業に呼ばれたり、スイス大使館でイベントを開いたり、マレーシアの文科省と交渉したり、ニューヨークの桜祭りでブースを設けたりと、鍜治と二人で世界を駆け巡り、得がたい体験をさせてもらった。ワシントンD.C.の日本大使館では宇宙飛行士の野口さんと面会し、「宇宙船の中で、ロシアの飛行士が数独を解いていましたよ。」というお話に感激した。

2006年3月には世界パズル連盟（World Puzzle Federation）が主催し、イタリアのルッカで第1回世界数独選手権が開かれた。この時の日本選手団団長は第3章に登場した西尾徹也である。彼自身は選手としても出場し、最年長ながら4位と健闘した。この数独選手権はその後も毎年一度開催されるようになり、今年（2018年）はチェコのプラハで第13回大会が開かれた。個人戦では日本人の森西亨太が昨年に続き、チャンピオンの座に輝き、日本チームも団体戦で優勝した。

また、魔方陣がそうであったように、数独も数学の研究対象としても注目された。9×9の盤面であるから、数独の問題は有限であるはずだ。一体何通りの数独が作れるのだろうか。オーストリアのコンピュータ研究所の計算によると、答えの盤面（つまり、全部の数字が埋まった状態）は、6．67×10の21乗というとんでもない数字であった。これを東工大の研究チームがスーパーコンピュータを4時間使ってすべての答えの盤面にナンバリングをしたそうだ。ちなみにこの数字は毎秒1万問という高速で解いていても、全部解くのに200億年では足りないということになる。

表出数字はどこまで減らせていけるのかという研究をした人もいる。アイルランドの数学者が「17個が最小である。」という結論をだした。つまり16個以下だと複数の解答が出てしまい、パズルとして成立しないのだ。今のところ、16個の問題は誰も作りだしていない。

さて、ウェイン・グールドとは2008年に再会した。日本のゲームソフト会社が数独大会を開き、そのゲストとして招待されたのだ。開口一番「怒っていないか？」とウェインは聞いてきた。彼はニコリの許可なく勝手に自作の数独を売り込んだことをとても申し訳なく思っていたらしい。もちろん、ニコリには彼の行為を咎める権利はなく、むしろ数独の名前を世界に広めたくれたことに感謝している。私たちは再会を祝し、ビールを飲みながらそんな話をした。これだけの短期間に世界を埋め尽くすだけの数独を供給できたのは、間違いなく自動生成というツールのおかげだ。ただ、ウェインは6年の歳月をかけて数独を研究し、その成果としてのプログラムを完成させたのだが、単にルールを理解しただけの初心者がプログラムを組み、かなりお粗末な数独が世界中に蔓延しているのは少し残念だ。

ウェインに「sudoku.comは順調か？」と尋ねたら、「売却しようと思っている。」という。彼のプログラムは飛ぶように売れ、その利益でニュージーランドの他に、ニューヨークや香港に5軒も家を建てた。だが、そのせいか分からないが彼の妻は家を出て行ってしまったそうだ。「もともと数独で商売をする気はなかった。静かな隠居生活を送るつもりがどうしてこうなったのか。」元判事はがっくりと肩を落とした。

中国古代の占いの数表が、スイスの数学者によって論理化され、それをアメリカの建築家がパズルにし、日本の出版社社長が本にしたところ、それを見たニュージーランドの裁判官がコンピュータプログラムにし、イギリスの新聞が掲載したら世界中に広まった。こんな物語を持つ数独は今も多くのファンを引きつけてやまない。これからも、子どもたちの論理的思考のトレーニングとして、高齢者の認知症予防のツールとして、そして何よりも暇つぶしとして、いつまでも愛されていくことだろう。

完